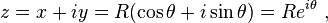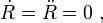Examples of circular motion include: an artificial satellite orbiting the Earth in geosynchronous orbit, a stone which is tied to a rope and is being swung in circles (cf. hammer throw), a racecar turning through a curve in a race track, an electron moving perpendicular to a uniform magnetic field, and a gear turning inside a mechanism.
Circular motion is accelerated even if the angular rate of rotation is constant, because the object's velocity vector is constantly changing direction. Such change in direction of velocity involves acceleration of the moving object by a centripetal force, which pulls the moving object toward the center of the circular orbit. Without this acceleration, the object would move in a straight line, according to Newton's laws of motion.
Contents[hide] |
[edit] Formulas for uniform circular motion
The vector relationships are shown in Figure 1. The axis of rotation is shown as a vector Ω perpendicular to the plane of the orbit and with a magnitude ω = dθ / dt. The direction of Ω is chosen using the right-hand rule. With this convention for depicting rotation, the velocity is given by a vector cross product as
[edit] Constant speed
In the simplest case the speed, mass and radius are constant.Consider a body of one kilogram, moving in a circle of radius one metre, with an angular velocity of one radian per second.
- The speed is one metre per second.
- The inward acceleration is one metre per square second.
- It is subject to a centripetal force of one kilogram metre per square second, which is one newton.
- The momentum of the body is one kg·m·s−1.
- The moment of inertia is one kg·m2.
- The angular momentum is one kg·m2·s−1.
- The kinetic energy is 1/2 joule.
- The circumference of the orbit is 2π (~ 6.283) metres.
- The period of the motion is 2π seconds per turn.
- The frequency is (2π)−1 hertz.
- From the point of view of quantum mechanics, the system is in an excited state having quantum number ~ 9.48×1035.
- The speed is v = r·ω.
- The centripetal (inward) acceleration is a = r·ω 2 = r −1·v 2.
- The centripetal force is F = m·a = r·m·ω 2 = r−1·m·v 2.
- The momentum of the body is p = m·v = r·m·ω.
- The moment of inertia is I = r 2·m.
- The angular momentum is L = r·m·v = r 2·m·ω = I·ω.
- The kinetic energy is E = 2−1·m·v 2 = 2−1·r 2·m·ω 2 = (2·m)−1·p 2 = 2−1·I·ω 2 = (2·I)−1·L 2 .
- The circumference of the orbit is 2·π·r.
- The period of the motion is T = 2·π·ω −1.
- The frequency is f = T −1 . (Frequency is also often denoted by the Greek letter ν, which however is almost indistinguishable from the letter v used here for velocity).
- The quantum number is J = 2·π·L h−1
[edit] Description of circular motion using polar coordinates
 is the radial vector from the origin to the particle location:
is the radial vector from the origin to the particle location: is the unit vector parallel to the radius vector at time t and pointing away from the origin. It is handy to introduce the unit vector orthogonal to
is the unit vector parallel to the radius vector at time t and pointing away from the origin. It is handy to introduce the unit vector orthogonal to  as well, namely
as well, namely  . It is customary to orient
. It is customary to orient  to point in the direction of travel along the orbit.
to point in the direction of travel along the orbit.The velocity is the time derivative of the displacement:
 has a time-invariant magnitude of unity, so as time varies its tip always lies on a circle of unit radius, with an angle θ the same as the angle of
has a time-invariant magnitude of unity, so as time varies its tip always lies on a circle of unit radius, with an angle θ the same as the angle of  . If the particle displacement rotates through an angle dθ in time dt, so does
. If the particle displacement rotates through an angle dθ in time dt, so does  , describing an arc on the unit circle of magnitude dθ. See the unit circle at the left of Figure 2. Hence:
, describing an arc on the unit circle of magnitude dθ. See the unit circle at the left of Figure 2. Hence: (or, in other words, along
(or, in other words, along  ) because any change d
) because any change d in the direction of
in the direction of  would change the size of
would change the size of  . The sign is positive, because an increase in dθ implies the object and
. The sign is positive, because an increase in dθ implies the object and  have moved in the direction of
have moved in the direction of  . Hence the velocity becomes:
. Hence the velocity becomes:The acceleration of the body can also be broken into radial and tangential components. The acceleration is the time derivative of the velocity:
 is found the same way as for
is found the same way as for  . Again,
. Again,  is a unit vector and its tip traces a unit circle with an angle that is π/2 + θ. Hence, an increase in angle dθ by
is a unit vector and its tip traces a unit circle with an angle that is π/2 + θ. Hence, an increase in angle dθ by  implies
implies  traces an arc of magnitude dθ, and as
traces an arc of magnitude dθ, and as  is orthogonal to
is orthogonal to  , we have:
, we have: orthogonal to
orthogonal to  . (Otherwise, the angle between
. (Otherwise, the angle between  and
and  would decrease with increase in dθ.) See the unit circle at the left of Figure 2. Consequently the acceleration is:
would decrease with increase in dθ.) See the unit circle at the left of Figure 2. Consequently the acceleration is:
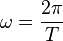



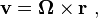
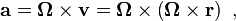
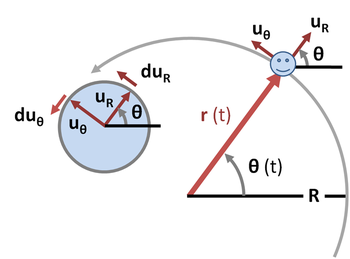
 and
and  in the unit vectors
in the unit vectors  and
and  for a small increment
for a small increment