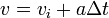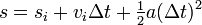GOT NIGHT CLASS . . =="

assalamualaikum .
harinie kami ade kelas waktu malam . haiiihh . .bulan pon bagi semangat taw nak belajar mlm2 . haha .

tp x pe la . demi untuk belajar .kami pegi jugak .naseb la haritu mOOd baek .yg dtg lambat x perlu denda .
tq so much dr . =) ape yg kami belajar malam tue . ini diaaa . .tajuk baru chapter 3 .KINEMATICS .
dengar cerita masuk test kan . OMG . semoga kami dapat buat . .AMINNN . .  nie la yg kami belajar . .


"Kinematics is the study of how things move. Here, we are interested in the motion of normal objects in our world. A normal object is visible, has edges, and has a location that can be expressed with (x, y, z) coordinates. We will not be discussing the motion of atomic particles or black holes or light.
We will create a vocabulary and a group of mathematical methods that will describe this ordinary motion. Understand that we will be developing a language for describing motion only. We won't be concerned with what is causing or changing the motion, or more correctly, the momentums of the objects. In other words, we are not concerned with the action of forces within this topic. "


ini ialah kinematic equation

dan ini 




 equation for linear motion .

  

Equations for Vertical Motion

Case I:

When a body is projected vertically downwards with initial velocity u then the equation describing motions are

    v = u + gt                                            ……(1)

    h = ut + 1/2 gt²                                    ……(2)

   v² = u² + 2gh                                         ……(3)

   h_n = distance covered in n^th second = u + 1/2 g(2n –1)  

Case II:

When body is falling down freely, then

    v = gt                                                ……(1)

    h = 1/2 gt²                                         ……(2)

   v² = 2gh                                              ……(3)

   h_n = 1/2 g(2n –1)                                  ……(4)

Case III:

When body is projected vertically upward with initial velocity u, then

   v = u –gt                                             ……(1)

   h = ut –1/2gt²                                      ……(2)

  v² = u² –2gh                                         ……(3)

  h_n = u –1/2g(2n –1)                                ……(4)

Greatest height attained = u²/2g                 ……(5)

Time to the greatest height = u/g                ……(6)

Time to a given height h = u/g ± √u²–2gh/g.

Notes:

• Time from any point on the path to the highest point is same as the time from the highest point to the given point when the body is returning.

Solved Example 1: 

A body is thrown vertically upward and rises to a height of 10 meters. Calculate (i) the velocity with which the body was thrown upwards and (ii) the time taken by the body to reach the highest point.

Solution:      

Let the body be thrown upwards with a velocity of 4 m/sec. Thus greatest height attained = u²/g meters.

   (i)  We have, greatest height = 10 meters

                        => u²/2g = 10 => u² = 196 => u = 14 m/sec

Hence, the required velocity of projection = 14 m/sec

   (ii) Time taken by the body to reach the greatest height = u/g sec = 14/9.8 = 10/7 sec.

Solved Example 2:

The greatest height attained by a particle projected vertically upwards is 19.6 meters. Find how soon after projection the particle will be at a height of 14.7 meter. 

Solution:       

Let u be the velocity of projection since at the greatest height, the velocity of the particle is zero.

     0² = u² –2g × 19.6 => u² = 19.6 × 19.6 => u = 19.6 m/sec

Suppose after time t the particle is at a height of 14.7 meter, then

   14.7 = 19.6t – 1/2 × 9.8 × t²

          = t² –4t+ 3 = 0 => (t –1) (t –3) = 0 => t = 1, 3

Thus, the particle will be at a height of 14.7 meter after 1 sec of its projection. It will also attain the same height after 3-seconds while coming downward after attaining the maximum height.

dan selepas itu kami di beri tugasan .

membuat sebanyak 22 soalan . for guys jwab soalan genap . n for girls jwab soalan ganjil .

soalan yg mencabar minda . not easy but take it easy . hahahaha . .

that's ALL . smoga rakan2 yang lain dpat menjawab soaln dgn jayanya . GOOD LUCK GUYS !

THANK YOU  FOR READING .

TODAY'S LESSON : DYNAMICS OF PARTICLE

assalamualaikum .

ini lah yang kami belajar semasa kelas petang tadi .

1.A force is a pull on a small object resulting from the interaction with another object .

2.Newton's first law

Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.

Law I: Every body persists in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed.

This law states that if the resultant force (the vector sum of all forces acting on an object) is zero, then the velocity of the object is constant. Mathematically stated:

Consequently:

• An object that is at rest will stay at rest unless an unbalanced force acts upon it.
• An object that is in motion will not change its velocity unless an unbalanced force acts upon it.

Newton placed the first law of motion to establish frames of reference for which the other laws are applicable. The first law of motion postulates the existence of at least one frame of reference called a Newtonian or inertial reference frame, relative to which the motion of a particle not subject to forces is a straight line at a constant speed. Newton's first law is often referred to as the law of inertia. Thus, a condition necessary for the uniform motion of a particle relative to an inertial reference frame is that the total net force acting on it is zero.

example .

1. What will happen to an object at rest if no force is applied?

2. What will happen to an object at rest if it is pushed, but there is a large frictional force acting on the object?

3. What will happen to the motion of an object that is pushed, and there is very little frictional force acting on the object?

4. What will happen to the motion of an object if there is a constant net force applied to it?

answers :

-nothing
-depends on the frictional force
-an object that has a force applied to it temporarily (a push) will travel at a constant speed infinitely until an outside force disrupts it such as friction. under most circumstances where friction is present an object will slowly decelerate and eventually stop
-if a constant net force is applied to an object, it will accelerate at a uniform rate until the force is removed. example: if you drop an object it will constantly accelerate downward due to the constant force of gravity pulling down on the object. the net force is always the same, yet the objects speed keeps increasing

THAT'S ALL .

THANK YOU . =)

GOOD LUCK DR. ARIF !

assalamualaikum .
minggu nie kami x belajar sebab Dr.Arif pegi maen bowling . kat melaka .
berita ini telah disampaikan oleh assistant dr.Arif . si cantik manis FARAHANAN .
hahahaa.  .
 .by the way . GOOD LUCK DR . all of us support u .

THANK YOU .

vector . .

QUESTION 1

 The diagram shows a stunt person of mass 82kg holding on to a rope. The rope on either side of the person makes an angle of 5 degrees to the horizontal

a) Determine the tension T in the rope.

b) What would be the consequence of making the angle between the rope and the horizontal equal to zero? 

Answers :

Let O be the point where the man or the weight force act towards earth.

Let the tension in  the ropes be T1  and T2.
Then the Component of tenesion force along and perpendicular dirctions should balance each other or thenet force is zero for equilibrium.

Horizontal componets T1cos(185) + T2cos(-5) = 0. This requires -cos5T1 and T2cos5 . Or the magnitudes of T1 = T2 = T say.
The vertical components: T1sin(185)+T2sin(-5) + 82g = 0
82 g = = 2T sin5.
T = 82g/2sin5, where g= 9.91 meter/s^2.

b)It is not possible as T = 82g/2sin0 =  82g/0 = infinite. No rope can bear this.



QUESTION 2

 A Crow flies in 2 successive displacements to a point that is 80m to the west. Its first displacement is 80m in a direction θ = 35degrees west of north.


a) What is the magnitude of its second displacement?


b)What is its direction as measured by the angle θ measured west from north?


answers :
Start from the origin.

The first displacement goes UP ( North ) and leans over to the left ( 35˚ West ) and is 80 m.

From the end of that line, the second displacement is down to x-axis line and along that line to the –80 mark.... which is the 80m West where the crow finishes up.

You need the length of the line that come down and its angle. ( and direction )

The direction is South 27.5˚ West.

That is easy because the triangle made by the two displacements and the x-axis, is an isosceles triangle with a vertex of 55˚ and the paired angles 62.5˚. Then you should see that you just have to take 35˚ from the top 62.5 ˚ and get the 27.5˚

The length - there are lots of ways to work this out.... easiest is the sine rule

A / sin A = B / sin B

80 / sin 62.5 = L / sin 55

L = 73.9 m




QUESTION 3

1. Fishing boat:
6m/s due North = wind velocity
10m/s due 240 degrees is the motor velocity
and the current velocity happens to be 3m/s due east.

The one below is for subtraction:
A spacecraft of mass 800kg is maneuvered by 2 rockets. The first rockets fires from the south west with a thrust of 1000N. The second fires from the south east with a thrust of 1000N.
What is the:
Net force on the spaceship
and the net acceleration of the spaceship?

Answers :

The simplest method is to split the vectors into Cartesian co-ordinates (North/South and East/West).

Problem 1:
Vector 1 is 6m/s North and 0m/s East/West
Vector 2 is at 240 degrees, aka West 30 degrees South. It breaks down into 10m/s * sin 30 degrees in the South direction plus 10m/s * cos 30 degrees in the West direction. These are 5.0 South and 8.66 West respectively.
Vector 3 is 0m/s North/South and 3m/s East.

Adding up the North/South components of the vectors, we get 6m/s North + 5m/s South + 0, which comes out to a total of 1m/s North.

Adding up the East/West components, we get 0 + 8.66m/s West + 3m/s East, which comes out to 5.66m/s West.

So the components of the final vector will be 1m/s North and 5.66m/s West. These are the vertical and horizontal lines in a triangle, with the third line being the final vector.
The size of the final vector will be the square root of the sum of the squares of the two components. sqrt (5.66^2 + 1^2) is 5.74m/s.

We already know (from the components) that the direction of the final vector will be somewhere between North and West, and will be more West than North. This means that the compass bearing will be between 270 degrees (West) and 315 degrees (North-West).

The cosine of the angle from due West will be the West component (5.66) divided by the total vector size (5.74). 5.66/5.74 is 0.986, and the inverse cosine of this is 9.58 degrees. Adding this to the West direction (270 degrees), we get a final direction of 279.58 degrees.

Given that the original question components were only accurate to one significant figure, your answer of "5.74m/s due 279.58 degrees" would become "6m/s due 280 degrees".

Problem 2:
Part A:
1000N from the south east towards the north west, plus 1000N from the south west towards the north east.

Vector 1 is 1000N * sin 45 degrees (707N) North plus 1000N * cos 45 degrees (707N) West
Vector 2 is 1000N * sin 45 degrees (707N) North plus 1000N * cos 45 degrees (707N) East

Final vector is 707N + 707N North (total 1414N North) plus zero newtons East/West
= 1414N due North (0 degrees)

The acceleration of the spaceship can be calculated from the equation F=ma

F = 1414N due North
m = 800kg
a = 1414 due North / 800kg = 1.77ms^-2 due North

Given that the original question components were only accurate to one significant figure, your answer of "1.77ms^-2 due North" would become "2ms^-2 due North".